Cheating Newton, again
It's been a while, almost a year since i've posted on this devlog/blog. Other projects happened. But this project ran into difficulties. The main problem is this: I want to create a 'cozy' universe, one where distances between planets, stars, etc. are small enough for real-time game play. Yet, I also wanted the game to feature somewhat realistic orbital mechanics. But Newton's laws don't play nice with my silly ideas. The inverse square law demands large distances between objects.
Newton
Just a quick recap, Newton's law of gravitational attraction states:
f = G * m1 * m2 / d^2
Here f is the attractive force experienced by a pair of bodies, G is the gravitational constant, m1 and m2 are the masses of the bodies and d is the distance between the bodies.
As can be seen, the force is proportional to the inverse of the distance squared. When the distance is multiplied by 2, the force is multiplied by is 1/4, etc.
This relationship results in orbits that are conic sections such as circles, ellipses, parabola and hyperbola. But only when just two bodies are considered. Because all bodies attract each other, we have to apply this formula for every pair of bodies in the system. In the general case, this results in chaos. In the real universe, this eventually sorts itself out: many small bodies collide and merge, until eventually (after a several hundred million years or so) star systems evolve where the only remaining objects are in mostly circular orbits.
In a previous post, I already explained that when generating star systems, I don't actually use Newton's laws, but I put the planets and moons and other objects on circular 'rails'. The radii of the circles, the velocity of the object, etc. are computed using Kepler's laws, which simply ignore the fact that all bodies attract each other. So two planets can pass in close proximity, but won't affect each others orbits.
But for the player and other dynamic objects (enemies, objects to interact with, etc.) I do need Newton's laws. A game where the player can only fly in a fixed circular obit would be boring.
So, what happens when the player attempts to orbit around a planet that's just being pulled along on rails? Well, that depends on the distance from the sun.
When we are far away from the sun, the gravitational influence of the sun is small. The planet itself will circle slowly around the sun. The player's orbit around the planet will be a conic, a neat solution from newton's laws. If the orbit is a circle or ellipse, the player can stay in this orbit as long as she wants without doing anything. Nice.
If however, our planet orbits closely to the sun, it's influence will be large. The planet itself will circle around the sun much faster than when it's far away, but this it not a problem in itself. The player is now affected by the gravity from the planet and the sun, which means the orbit is not a neat conic solution, and in general not circular or ellipsoid. In fact, after a few orbits, the player will likely crash into the planet. In severe cases, close the the sun, it won't even be possible to orbit the planet at all.
In this video, you can see that the player can't get in a stable orbit and must keep adjusting her speed, or crash.
Let's have a closer look at the problem.
In the image below, the situation is sketched. We have a blue planet orbiting around a yellow sun. We want the player to orbit around the blue planet as indicated by the dashed black ellipse. In the upper part of the image, the forces on the player are sketched: in yellow the force from the sun, in blue the force from the planet, and in red, the sum of the two forces. Looking at the blue line, we can see that the forces from the planet on the player to the left and right of the planet are the same. But when we consider the total force in the red line, it's clear that when the player is closer to the sun, the total force is higher then when the player is on the other side of the planet, further from the sun. This results in a skewed orbit that will eventually spiral into the planet, crashing the player.
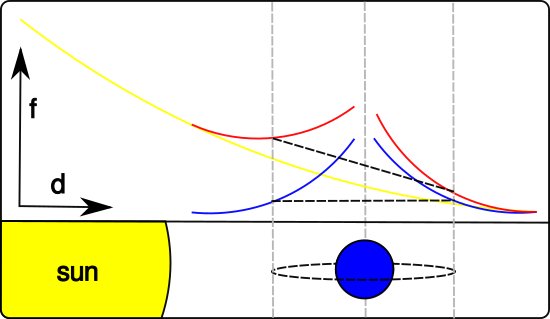
In the real solar system, relative distances are so large that the influence of the sun in a large area around a planet is almost exactly the same. So orbits around planets really are quite stable. In our cozy universe, where everything is close together, the skewed effect of the force from the sun is a problem.
So, we'll have to cheat.
More cheating
I already 'cheated' when I placed planets and other bodies on circular rails. I'm not putting the player on rails, but we might eliminate the problem of unstable orbits by considering only one other body when calculating forces on the player. If the player is only affected by the force of one body, the player's orbit will be stable.
In previous iterations of this project, I already did some optimization when computing forces; only those bodies that where close enough to have a significant effect where considered. Each body was assigned a region of influence. The more massive the object, the greater its region of influence.
Now we go even further; only once body is considered, namely: the body closest to the player. But that cannot work, can it? No, we cannot completely ignore the other forces. If the player is in orbit around some planet, and that planet is itself in orbit around the sun, then the player must also be in orbit around the sun, at the same speed as the planet.
One solution for this might be to consider the player to be in a coordinate system centered on the planet. When the planet is moved, the coordinate system of the player is moved with it. This is something that is easily done in most game engines, where objects can be nested in a hierarchy. However, this approach doesn't really work with the physics engine in the system I'm using (Godot). When the planet moves, the game engine will move the player, but the physics engine doesn't understand that a force on the player is needed to change its velocity, resulting in glitches and jerky movement.
The approach I've taken is to keep the player in the global coordinate system, and to compute the force on the player needed to match the orbit of the body that the player is closest too. So, two forces act on the player: the force from the body that the player is closest too, and the force that it would feels if it were orbiting in the same way as that body around it's parent. Because the body is in a circular orbit, this force is always pointed towards the center of the orbit, and the magnitude is constant, computed using Newton's law of attraction with d equal to the radius of the orbit.
The forces experienced by a player in orbit are sketched below. We don't directly apply the attractive force of the sun (yellow) on the player. Instead, we use the force from the nearest body (blue) and add a constant force (green), corresponding to the force from the sun as would be experienced in the center of the planet. As can be seen in the image, the force experienced by the player(red) is the same on both sides of the planet, resulting in a stable orbit. Hurray!
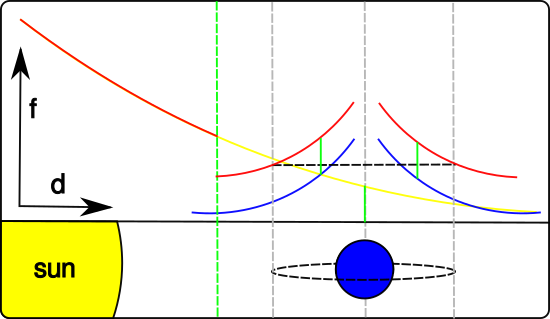
Then there is a unfortunate side effect, which can be seen at the green dotted line, where the sun and the planet are the same distance from the player: there is a discontinuity, a sudden jump in the force experienced. Although the player probably won't really notice or mind this effect, it's a problem when computing the players trajectory. Doing forward integration over functions with discontinuous results in errors in the result, and during the game this is visible in the plotted trajectory wobbling or jumping around. So, as a final step, we should add some smoothing to the function around the discontinuity. The result is a function that looks like this:
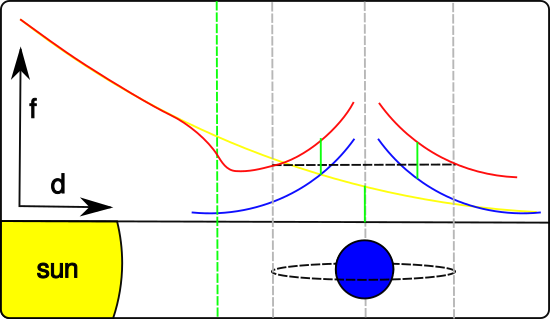
There are some more complications. When the hierarchy of orbiting bodies is deeper than the two bodies shown in these examples, there are also the forces from the bigger objects higher up in the hierarchy to be considered. I've not illustrated those here, but the basic idea is the same. Instead of one constant force, there are more constant forces added, to keep the player in orbit around all ancestor bodies in the hierarchy. Also, in 2D the force is not really constant, only its magnitude; the direction of the force changes as the player moves. That's all details.
So we are cheating the laws of gravity a bit. But it works! Here's a video showing the result. Look at how close those planets are to that huge sun! In the real universe, it would never be possible for any of those orbits to exist...
Amazing Space Adventure
adventures with Newton
| Status | In development |
| Author | kwikrick |
| Genre | Adventure |
| Tags | Gravity, Space Sim |
More posts
- A frame around the universeApr 22, 2023
- Kepler, Newton, GodotApr 06, 2023
- PaintingsApr 02, 2023
- Amazing Space Adventure #2Apr 02, 2023
- Amazing Space AdventureApr 02, 2023
Leave a comment
Log in with itch.io to leave a comment.